note

1. Introduction

目前存在集中不同的机器学习算法，大概可以分为两种，一种是监督学习，另一种是无监督学习。

• 监督学习：给定已有正确的数据集，运用学习算法，算出更多正确的结果。

  • 回归问题：算法的输出为连续的值，即定量输出

  • 分类问题：算法的输出为离散的值，即定性输出

• 无监督学习：没有正确答案，只有一个数据集，让算法从中找到某种结构，典型例子就是聚类算法。

  鸡尾酒晏例子：看图

  

用算法把声音和音乐分开，使用Octave仅需要一行代码：

[W,s,v] = svd((repmat(sum(x.*x,1),size(x,1),1).*x)*x');

2. 单变量线性回归(Linear Regression with One Variable)

房价例子（监督学习/回归问题）：给定正确的俄勒冈州波特兰市的住房价格数据集，预测Size条件下房价Price的值；看图：

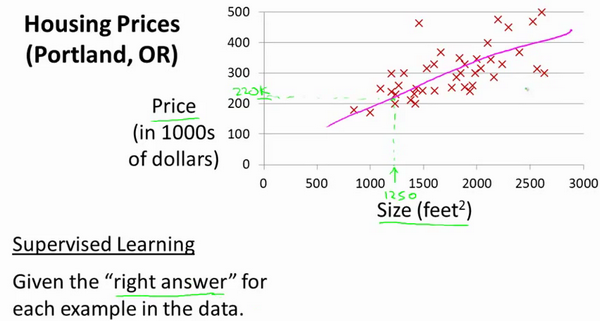
这个回归问题的数据集如图所示：

那么，在这里，我们把这个问题标记如下：

• 代表训练集中实例的数量

• 代表特征/输入变量

• 代表目标变量/输出变量

• )代表训练集中的实例

• 代表第i个观察实例

• 代表学习算法的解决方案或函数也称为假设（hypothesis）

这个是监督学习的工作方式，其中根据的输入得出值，那么也可以说是从到的函数映射

我将选择最初的使用规则代表hypothesis，因而，要解决房价预测问题，我们实际上是要将训练集“喂”给我们的学习算法，进而学习得到一个假设，然后将我们要预测的房屋的尺寸作为输入变量输入给，预测出该房屋的交易价格作为输出变量输出为结果。那么，对于我们的房价预测问题，我们该如何表达？ 一种可能的表达式为：，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题。

那么代价函数(Cost Function)就为：=\frac{1}{2}m\sum_{i=1}^{m}(h_{\theta&space;}(x^{(i)})-y^{(i)})^2) 这里的的参数无论怎么改变，其实都是一样的，只不过最后的曲线会小一些罢了

我们的目标就是调整和使代价函数的结果最小，即使得出的函数曲线尽量贴合数据

上述例子中相关的式子：

我们将简化掉得到=\theta&space;_{1}x)，代价函数在时，=0)，即h正确拟合，左边这条函数曲线（直线）对应了所有的数据

2.1 轮廓图（等高线图）

略

2.2 梯度下降(Gradient Descent)

梯度下降是很常用的最小化函数的方式；我们在这里使用梯度下降算法求代价函数的最小值。

梯度下降的思想是，给定一系列θ值，然后我们找到一个能让代价函数下降最多的值的集合，然后重复这个步骤知道找到局部的最小值（local minimum），但是我们没有尝试完所有的组合，所以这个最小值不是全局最小值（global minimum）

梯度下降的过程如图所示：

批量梯度下降（batch gradient descent）算法的公式为：

• α是学习率（learning rate），它决定了我们让代价函数下降的步长。

• 在批量梯度下降中，我们每一次都会让所有的参数同时变化（即所有的参数减去学习速率乘以代价函数的导数）

• 和其实是微分项

2.2.1 梯度下降的直观理解

举例，我们的梯度下降算法如下：

)

描述：对赋值，使得按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

对于这个问题，变成了求下图红色斜线的斜率，也就是那条红色的切线，当我们娶到如图中的切点时，我们求导得到了正斜率，这个式子就变成了) 通过它，我们得到了一个新的，这个等于减去一个正数的斜率乘以

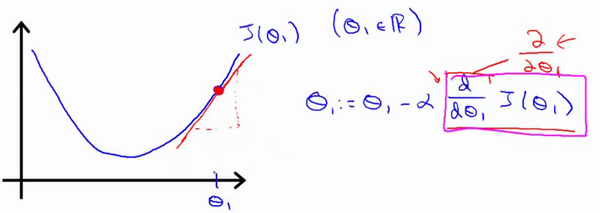
这里涉及到了两个问题：

• 太大或者太小会出现什么情况？

• 如果直接把放在局部最低点，接下来梯度下降算法接下来该怎么做？

首先第一个问题，太大的话梯度下降法可能会直接越过最低点，甚至无法收敛 太小的话，即我的学习速率太小，需要很长时间才能移动到最低点；

第二个问题已经到最低点的时候，对这个点求导为0，即是这条上面那条红色斜线的斜率为0；那么这个时候我们的梯度下降算法式子为

即，那么，到这里，梯度下降算法其实什么都没做，他也不会改变参数的值。那么这也解释了，为什么学习速率保持不变的时候，梯度下降也会收敛到最低点。

那么，在梯度下降的过程中，式子是怎么变化的呢？

举一个例子，如图代价函数)，我们要找到它的最小值，首先初始化我们的梯度下降算法，可以看出导数项对应的斜率是蛮陡的，但是当迭代多次之后，我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是梯度下降的做法。所以实际上没有必要再另外减小α

这就是梯度下降算法，你可以用它来最小化任何代价函数

2.2.2 梯度下降的线性回归

我们谈到关于梯度下降算法，梯度下降是很常用的算法，它不仅被用在线性回归上和线性回归模型、平方误差代价函数。这部分内容，我们要将梯度下降和代价函数结合。我们将用到此算法，并将其应用于具体的拟合直线的线性回归算法里。

梯度下降算法和线性回归算法比较如图：

对我们之前的线性回归问题运用梯度下降法，关键在于求出代价函数的导数，即： =\frac&space;{\partial&space;}{\partial&space;\theta_{j}}&space;\frac&space;{1}{2m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})^{2})

时：=\frac&space;{1}{m}\sum{i=1}^{m}(h{\theta}(x^{(i)})-y^{(i)}))

时：=\frac&space;{1}{m}\sum{i=1}^{m}((h{\theta}(x^{(i)})-y^{(i)})\cdot&space;x^{(i)}))

应用梯度下降算法把上式改写成这样：

Repeat {

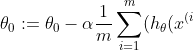})-y^{(i)}))

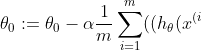})-y^{(i)})\cdot&space;x^{(i)}))

}

这个算法叫做批量梯度下降，意思是指，在梯度下降算法的过程中，用到了所有的训练样本，即在公式中，每一次求导都要对结果求和，求了m次。

但在线性代数中，有一种计算代价函数最小值的方法，它可以在不需要多步梯度下降的情况下，也能解出代价函数的最小值，这是另一种称为正规方程(normal equations)的方法。实际上在数据量较大的情况下，梯度下降法比正规方程要更适用一些。

3. 线性代数回顾（Linear Algebra）

• 矩阵和向量定义

略

• 加法和矩阵标量乘法

行列相等的可以加，其他略

• 矩阵向量乘法

矩阵乘法：

矩阵乘以矩阵，变成矩阵。

比如：

矩阵乘法的性质：

矩阵的乘法不满足交换律：

矩阵的乘法满足结合律。即：=(A\times&space;B)&space;\times&space;C)

单位矩阵：在矩阵的乘法中，有一种矩阵起着特殊的作用，如同数的乘法中的1,我们称这种矩阵为单位矩阵．它是个方阵，一般用或者表示；单位矩阵从左上角到右下角的对角线（称为主对角线）上的元素均为1以外全都为0。如：

对于单位矩阵有下式

• 逆、转置（Inverse and Transpose）

矩阵的逆：如矩阵是一个的矩阵，对于它的逆矩阵有，

矩阵的转置：设为阶矩阵（即行列），第行列的元素是)，即：)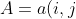

定义的转置为这样一个阶矩阵，满足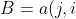)，即=a(j,i)),记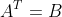。（有些书记为A'=B）

例：

矩阵的转置基本性质：

}^{T}}={{A}^{T}}\pm&space;{{B}^{T}})

}^{T}}={{B}^{T}}\times&space;{{A}^{T}})

}^{T}}=A)

}^{T}}=K{{A}^{T}})