# note

\[TOC]

## NN Representation

![1572487824128](/files/-Lsz33Ia5dbxWbM39Vo1)

我们有输入特征$x\_1$、$x\_2$、$x\_3$，它们被竖直地堆叠起来，这叫做神经网络的**输入层**。它包含了神经网络的输入；然后这里有另外一层我们称之为**隐藏层**。图中的最后一层只由一个结点构成，而这个只有一个结点的层被称为**输出层**，它负责产生预测值。

隐藏层的含义是在训练集中，这些中间结点的准确值我们是不知道到的，也就是说你看不见它们在训练集中应具有的值。你能看见输入的值，你也能看见输出的值，但是隐藏层中的东西，你是无法看到的。

![1573710301084](/files/-LtdHv9HWTmC757iBBnF)

我们约定input layer不算做一个层，所以上图是一个两层的网络。hidden layer记作$a^{\[1]}$，outputlayer记作$a^{\[2]}$，$a$代表激活的意思，它意味着网络中不同层的值会传递到他们后面的层中，$a^{\[1]}$中有三个节点，我们把第一个节点记作$a^{\[1]}\_1$，剩下的类推。

$$
a^{\[1]}=\begin{bmatrix}
a^{\[1]}\_1\\
a^{\[2]}\_2\\
a^{\[3]}\_3\\
\end{bmatrix}
$$

$\bold w,\bold b$是$(4,3)$和$(4,1)$维的向量：

​ 注意，$\bold w$是转置后的向量。

* $\bold w$的4代表4个单元，3代表3个对应着特征$x$的权重变量，即$\bold w\_1^{\[1]}$为$(1,3)$的向量；
* $\bold b$的4对应着4个单元中b的值。

## NN‘s Output Computing

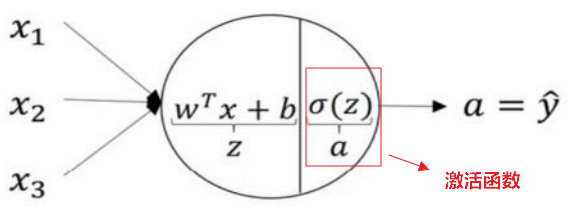
神经网络的计算，以LR为例，如下图所示：用**圆圈**表示神经网络的计算单元， 逻辑回归的计算有两个步骤，首先你按步骤计算出$z$，然后在第二步中你以**sigmoid**函数为激活函数计算$a$，一个神经网络只是这样子做了好多次重复计算。 计算出每个神经元的值，然后传播给下一层计算。式子略。

![1572490407636](/files/-Lsz33IiKKLxebogEX47)

**向量化计算**上述步骤， 向量化的过程是将神经网络中的一层神经元参数纵向堆积起来，每个向量$\bold w$对应着一个单元，把这些向量堆积起来，就会得到$\bold w$的矩阵，用$w^{\[n]}$表示某一层的神经网络。

先计算$z$：

$$
\left\[
\begin{array}{c}
z^{\[1]}*{1}\\
z^{\[1]}*{2}\\
z^{\[1]}*{3}\\
z^{\[1]}*{4}\\
\end{array}
\right]
\=
\overbrace{
\left\[
\begin{array}{c}
...W^{\[1]T}*{1}...\\
...W^{\[1]T}*{2}...\\
...W^{\[1]T}*{3}...\\
...W^{\[1]T}*{4}...
\end{array}
\right]
}^{W^{\[1]}}
\*
\overbrace{
\left\[
\begin{array}{c}
x\_1\\
x\_2\\
x\_3\\
\end{array}
\right]
}^{input}
\+
\overbrace{
\left\[
\begin{array}{c}
b^{\[1]}\_1\\
b^{\[1]}\_2\\
b^{\[1]}\_3\\
b^{\[1]}\_4\\
\end{array}
\right]
}^{b^{\[1]}}
$$

之后带入到sigmoid：

$$
a^{\[1]} =
\left\[
\begin{array}{c}
a^{\[1]}*{1}\\
a^{\[1]}*{2}\\
a^{\[1]}*{3}\\
a^{\[1]}*{4}
\end{array}
\right]
\= \sigma(z^{\[1]})
$$

隐藏层$a^{\[1]}$完成，接下来输出层也是一样的：

$$
Z^{\[2]}=w^{\[2]}a^{\[1]}+b^{\[2]}
\\
a^{\[\[2]]}=\sigma(z^{\[2]})
$$

![1573713915170](/files/-LtdHv9LPdPG8Ca8yre7)

## Activation functions

在隐层接一个线性变换后 ，再接一个非线性变换(如sigmoid)，这个非线性变换叫做**传递函数或者激活函数**。上面的例子用的都是逻辑回归的Sigmoid激活函数，如果还不明白激活函数在哪，可以看下面这幅图。

![](http://wx3.sinaimg.cn/mw690/00630Defly1g5h3pqzw0sj30g5068wfi.jpg)

1. **sigmoid函数**

   ![image](https://ws2.sinaimg.cn/large/00630Defly1g2x34jlnrrj306g0590st.jpg)

   !\[]\(<https://latex.codecogs.com/gif.latex?a=g(z)=\frac{1}{1+e^{-z}}>)

   !\[]\(<https://latex.codecogs.com/gif.latex?g(z)^{'}=\frac{d}{dz}g(z)=a(1-a>))
2. **tanh(双曲正切)函数**

   事实上，**tanh** 函数是 **sigmoid** 的向下平移和伸缩后的结果。对它进行了变形后，穿过了(0,0)点，并且值域介于+1 和-1 之间。但有一个例外：在二分类的问题中，对于输出层，因为𝑦的值是 0 或 1，所以想让𝑦^的数值介于0和1之间，而不是在-1和+1之间。所以需要使用**sigmoid**激活函数。

   ![](http://wx1.sinaimg.cn/mw690/00630Defgy1g5nm3dsq7aj30ad02zq2y.jpg)

   **sigmoid**函数和**tanh**函数两者共同的缺点是，在𝑧特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于 0，导致降低梯度下降的速度。
3. **ReLu(修正线性单元)函数**

   只要𝑧是正值的情况下，导数恒等于 1，当𝑧是负 值的时候，导数恒等于 0，当=0的时候可以设为0/1因为正好等于1的概率非常小，对于全局影响不大，所以取什么值无所谓。

   ![image](https://wx4.sinaimg.cn/large/00630Defly1g2x3f01a0gj306d04xmx7.jpg)

   $$
   a=max(0,z)
   $$

![](http://wx3.sinaimg.cn/mw690/00630Defgy1g5nm5d67dbj30ar03h3yi.jpg)

这有一些选择激活函数的经验法则： 如果输出是 0、1 值（二分类问题），则输出层选择 **sigmoid** 函数，然后其它的所有单 元都选择 **Relu** 函数。

1. **softmax激活函数**

   * 非线性变换之前计算：!\[]\(<https://latex.codecogs.com/gif.latex?z^{(l)}=W^{(l)}a^{(l-1)}+b^{(l)}>)
   * 经过非线性变换，临时变量：!\[]\(<https://latex.codecogs.com/gif.latex?t=e^{z^{(l)}}>)
   * $a^{l}=\frac{t*i}{\sum*{j=1}^{n}t\_i}$归一化
   * $a^l$表示的就是第几个类别的概率值，这些**概率值和为1**

   之前，我们的激活函数都是接受单行数值输入，例如 **Sigmoid** 和 **ReLu** 激活函数，输入一个实数，输出一个实数。**Softmax** 激活函数的特殊之处在于，因为需要将所有可能的输出归一化，就需要输入一个向量，最后输出一个向量。

   **hardmax** 函数会观察𝑧的元素，然后在𝑧中最大元素的位置放上 1，其它位置放上 0，**Softmax** 所做的从𝑧到这些概率的映射更为温和。

   **Softmax** 回归将 **logistic** 回归推广到了两种分类以上。

### 优缺点

* 在𝑧的区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于0，在程序实现就是一个 **if-else** 语句，而 **sigmoid** 函数需要进行浮点四则运算，在实践中，使用 **ReLu** 激活函数神经网络通常会比使用 **sigmoid** 或者 **tanh** 激活函数学习的更快。
* **sigmoid** 和 **tanh** 函数的导数在正负饱和区的梯度都会接近于 0，这会造成梯度弥散，而 **Relu** 和 **Leaky ReLu** 函数大于 0 部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，**Relu** 进入负半区的时候，梯度为 0，神经元此时不会训练，产生所谓的稀疏性，而 **Leaky ReLu** 不会有这问题) 𝑧在 **ReLu** 的梯度一半都是 0，但是，有足够的隐藏层使得 z 值大于 0，所以对大多数的 训练数据来说学习过程仍然可以很快。&#x20;

### [BP](<https://blog.csdn.net/fendouaini/article/details/79789440 >)

![1576131642585](/files/-Lxuc6d3NkByR1JhwDjN)

[反向传播的一个直观理解](<https://www.open-open.com/lib/view/open1441541390219.html#articleHeader3 >)

### 训练的优化

梯度下降如果：

* 每次都在整个数据集上计算Loss和梯度的话
  * 计算量大，内存承载不住
  * 下降方向确定，步长依然不变的话依然会慢

优化：

* 随机梯度下降

  每次使用一个随机样本，不使用整个数据集
* Mini-Batch

  每次使用一小部分随机采用样本，不使用整个数据集

缺点：

* 存在震荡问题，batch-size越大越不明显，反之随机梯度下降最明显。
* 局部极值和鞍点(saddle point)问题
  * 局部极值：learning\_rate是个关键
  * 如图，导数为0，导致参数得不到更新，这个

    ![1576132619797](/files/-Lxuc6d58HqcG-t-5z3Z)

为了解决问题，提出SGD（动量梯度下降）：

![1576133043677](/files/-Lxuc6d71MF07Cx9PDPK)

优点：

* 开始训练时，积累动量，加速训练
* 局部极值附近震荡时，梯度为0，由于动量，跳出陷阱
* 梯度改变方向时，动量缓解动荡

如图所示：

![1576133256499](/files/-Lxuc6d96OXuDHDCVH6d)


---

# Agent Instructions: Querying This Documentation

If you need additional information that is not directly available in this page, you can query the documentation dynamically by asking a question.

Perform an HTTP GET request on the current page URL with the `ask` query parameter:

```
GET https://jon-xia.gitbook.io/workspace/ji-qi-xue-xi-41/wu-en-da-deeplearning/neural-networks-and-deep-learning/week3/note.md?ask=<question>
```

The question should be specific, self-contained, and written in natural language.
The response will contain a direct answer to the question and relevant excerpts and sources from the documentation.

Use this mechanism when the answer is not explicitly present in the current page, you need clarification or additional context, or you want to retrieve related documentation sections.